从数学角度分析下次图像看缺陷分析的逻辑
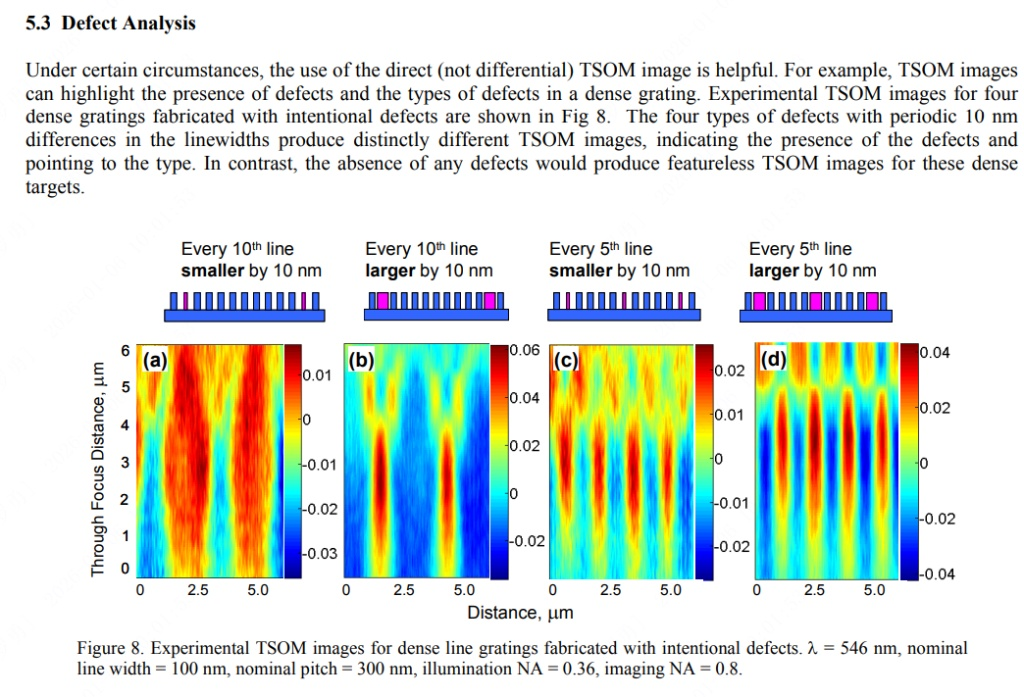
从数学和信号处理的角度来看,TSOM(离焦扫描光学显微术)对缺陷的分析逻辑,本质上是一个**“空间频率滤波”与“相位-强度转换”**的过程。
我们可以将图像中的现象拆解为以下几个数学逻辑步骤:
1. 信号分解:载波与包络 (Carrier vs. Envelope)
首先,我们将光栅看作一个一维的空间函数 。
- 理想光栅 (载波):是一个高频周期函数。
其中基频 。在本例中,,这是一个非常高的空间频率。由于显微镜的光学分辨率限制(衍射极限 ),这个高频载波可能接近截止频率,成像时往往只表现为均匀的背景灰度(直流分量 DC)。
- 缺陷函数 (调制波): 缺陷并不是随机的,而是周期性出现的(每10条或每5条)。这引入了一个新的、低频的“调制信号” 。
- 图 (a)/(b) 的缺陷周期:。频率 。
- 图 (c)/(d) 的缺陷周期:。频率 。
数学结论 1: 光学系统可能看不清 300 nm 的单根线条,但能轻松“看清” 3000 nm 或 1500 nm 的宏观周期变化。TSOM 图像实际上是在对这个低频的“缺陷包络”进行成像。
2. 差分与线性叠加 (Linearity & Contrast)
图谱颜色的深浅代表光强 的变化。对于微小缺陷,我们可以使用微扰理论近似。
设光场 ,其中 是理想光栅的背景场, 是缺陷产生的散射场。 探测到的强度为:
- 是常数背景。
- 对于微小缺陷可以忽略(二阶小量)。
- **干涉项 ** 是主导项。
数学结论 2 (正负相关性):
- 图 (a) vs 图 (b):
- (a) 线宽减小 (),相当于在原位置叠加了一个“负”的散射场 。
- (b) 线宽增加 (),相当于叠加了一个“正”的散射场 。
- 这导致干涉项符号翻转。因此,图 (a) 中的红色高亮区域(强度增强),在图 (b) 中变成了蓝色深陷区域(强度减弱)。数学上表现为相位的 翻转。
3. Z轴的频域演化 (Through-Focus Evolution)
为什么图像在纵轴(Z轴)上会呈现出拉长的“纺锤形”或震荡条纹?这涉及光在传播过程中的菲涅尔衍射 (Fresnel Diffraction)。
在频域中,光沿 Z 轴传播相当于乘以一个传递函数 :
- 的变化引入了随空间频率 平方的相位因子变化。
- 这种相位变化会将物体的幅度信息转化为强度信息(类似于相衬显微镜原理),并且随着 的增加,不同空间频率的分量会发生干涉相长或相消。
数学结论 3 (古伊相移 Gouy Phase Shift 的类比): 图中的垂直条纹(红色或蓝色斑块)实际上是缺陷产生的散射光在不同离焦平面上的三维点扩散函数 (3D PSF) 的切片。
- 周期性重复:横轴上的重复是因为缺陷本身是周期排列的。
- Z轴拉伸:表明该缺陷特征具有较长的焦深(Depth of Focus),这通常是低数值孔径(Low NA)成分或低频成分的特征。
4. 频率倍增效应 (Frequency Doubling)
对比图 (a)/(b) 与图 (c)/(d):
- 输入信号频率:(c) 的缺陷密度是 (a) 的两倍(每5行 vs 每10行)。
- 输出图像频率:观察 TSOM 图像的横轴,(c) 中亮暗条纹的密集程度显然也是 (a) 的两倍。
这验证了该成像系统在低频段是线性的——输入信号(缺陷分布)的频率直接映射到了输出图像的强度分布频率上。
总结
从数学逻辑上看,这张图说明了 TSOM 方法实际上是一种**“频谱搬移与放大”**技术:
- 降频:利用周期性缺陷形成的莫尔条纹 (Moiré-like effect) 或超晶格 (Super-lattice) 效应,将无法分辨的高频光栅细节 () 转化为可分辨的低频缺陷信号 ()。
- 符号敏感:利用干涉项的线性特性,通过强度的正负(红/蓝)直接判断线宽是变大还是变小(导数的符号)。
- Z轴层析:利用离焦带来的相位演化,增强了对微弱相位物体(由微小尺寸变化引起)的对比度。
菲涅尔衍射 (Fresnel Diffraction):现象与数据分析
菲涅尔衍射,又称近场衍射。简单来说,它是当光经过物体(如微小孔洞、边缘或光栅)后,在距离物体较近的区域内形成的复杂光影图案。
与我们熟悉的“夫琅禾费衍射”(远场衍射,如激光笔照出的光斑)不同,菲涅尔衍射的图案会随着距离(Z轴)的变化而剧烈演变。
1. 现象描述:光场的“近身肉搏”
想象你把一个网格放在手电筒前,然后把一张白纸从网格后面紧贴着慢慢向后移:
- 极近处 (几何投影区): 你看到清晰的网格影子(黑白分明)。
- 稍远处 (菲涅尔区): 影子的边缘开始模糊,出现明暗相间的条纹。更神奇的是,原本黑色的线条中心可能会亮起来,白色的空隙中心可能会变暗。图案在不断“震荡”变化。
- 极远处 (夫琅禾费区): 图案稳定下来,只随距离放大,不再改变形状。
核心特征:
- 非保形性: 衍射图案与原物体形状不完全像(比如圆孔可能衍射出中心亮斑,也可能衍射出中心黑点,取决于距离)。
- 演化性: 只要 Z 轴(距离)改变一点点,光强分布 就会发生显著变化。
2. 数学模型:二次相位调制
从数据分析的角度,菲涅尔衍射可以看作是一个线性系统对输入光场进行了一次卷积运算。
假设物体的光场分布为 ,传播距离 后的光场 近似为:
其中卷积核 是一个二次相位因子(Chirp Function):
数据分析含义: 这个公式告诉我们,光在传播过程中,不同空间位置的相位发生了“弯曲”。这就好比把一张原本平整的图片,放在哈哈镜前不断拉伸和扭曲。
3. 数据分析逻辑:如何从“光斑”看出“缺陷”?
回到您之前的 TSOM 缺陷分析,其本质就是对菲涅尔衍射数据的逆向分析。
A. 数据集构建:3D 光强立方体
我们不再看一张图,而是采集一个数据立方体 。
- 切片 (Slicing): 固定 (横向位置),观察 (沿轴向的变化)。这被称为“轴向光强分布”。
- 特征 (Feature): 菲涅尔衍射对 极其敏感。一个 10nm 的尺寸变化,会改变波前的曲率,导致在某个特定的 处,干涉条纹发生相移或反转。
B. 关键分析指标
在分析衍射图谱时,通常关注以下数学特征:
- Talbot 效应 (自成像效应):
- 现象:对于周期性结构(如之前的光栅),在特定的菲涅尔距离 ,光场会“复制”原物体的图像。
- 分析点:如果您在 处看到的图像模糊或扭曲了,说明周期结构有缺陷。
- 古伊相移 (Gouy Phase Shift):
- 现象:光束在经过焦点附近时,会产生额外的 相位突变。
- 分析点:缺陷通常会表现为图谱中颜色的翻转(如前图中的红变蓝)。这对应了衍射积分中相位项的正负号变化,直接指示了缺陷是“凸起”还是“凹陷”。
- 对称性分析 (Symmetry Metric):
理想情况:完美的线条衍射图案通常关于焦平面是对称的。
缺陷情况:如果存在侧壁倾斜(Asymmetry),衍射图案在焦前和焦后会呈现不对称性。
公式:
如果 ,说明结构有不对称缺陷。
总结:菲涅尔衍射的数据视角
| 物理视角 | 数据/算法视角 | 应用价值 |
|---|---|---|
| 近场光波的干涉 | 卷积运算与相位解缠 | 将不可见的微小相位变化(纳米级深度/宽度)转化为可见的强度变化。 |
| 随距离变化的图案 | 沿 Z 轴的时间序列分析 | 通过 Z 轴扫描,哪怕光学分辨率不够,也能通过“光强震荡的节奏”推算出物体尺寸。 |
所以,您看到的那些彩色的“纺锤形”图案,本质上就是缺陷引起的菲涅尔衍射波,在 Z 轴空间上留下的轨迹。